Eu penso que você pensa que eu penso que você pensa… que isso tudo é muito complicado!
1 Introdução
Para quem não conhece, a Wikipédia descreve a Teoria dos Jogos como o estudo de modelos matemáticos ilustrando conflitos e cooperações entre agentes racionais. Basicamente, é o uso de ferramentas da lógica e da matemática para entender comportamentos estratégicos (1). Dentro dessa enorme teoria tem “comportamento
estratégico para todos os gostos e estilos”: é dilema dos prisoneiros, é equilíbrio de Nash, é modelo Lotka Volterra, ultimatum game…
Normalmente, a Teoria dos Jogos procura descrever um aspecto normativo de comportamento. Isso significa que essa teoria procura descrever a MELHOR estratégia, a coisa mais lógica a se fazer. Mas a Economia Comportamental, Sociologia, Psicologia e ciências afins mostram que muitas vezes o ser humano não escolhe o lógico… Essas áreas mostram um novo mundo descritivo, que tenta estudar o que o ser humano realmente faz.
As interações entre essas duas áreas mostram ideias realmente fascinantes e vamos tentar mostrar um pouco disso aqui. Nesse texto vamos falar um pouco sobre um dos temas mais complexos de Teoria dos Jogos, o Conhecimento Comum. Após isso, usaremos o Conhecimento Comum para discutir um dos Jogos mais estudados pela Economia, Acerte a Média – também conhecido como Concurso de Beleza. Para finalizar, um toque de Economia Comportamental/ Psicologia com Cognição Level K e o que os seres humanos realmente
escolhem nesse Jogo.
2 Conhecimento Comum
Assim como tudo na lógica e na matemática, muitos modelos da Teoria dos Jogos se tornam extremamente complicados e usam construções bem complexas. Uma das construções mais importantes e mais difíceis de entender é a ideia de Conhecimento Comum.
O Conhecimento Comum para Teoria dos Jogos é um tipo de conhecimento muito especial. É Conhecimento Comum aquilo que todo mundo sabe, que todo mundo sabe que todo mundo sabe, que todo mundo sabe que todo mundo sabe que todo mundo sabe… e assim vai ad infinitum. Essas interações muitas vezes criam problemas de lógica complicadíssimos. Vamos tentar descrever uma situação “simples”:
Três garotas estão usando chapéus que podem ser vermelhos ou brancos e estão sentadas em círculo de modo que conseguem ver os chapéus das outras mas não o próprio. Para deixar mais peculiar esse exemplo, considere que todas as garotas estão usando chapéus vermelhos. Quando uma quarta pessoa pergunta se as garotas sabem identificar a cor de seu próprio chapéu, a resposta é negativa, já que ninguém pode ver o próprio chapéu. Mas se essa quarta pessoa fala que há pelo menos um chapéu vermelho -fato que todas sabem já que conseguem ver os outros dois chapéus vermelhos- e volta a perguntar UMA POR UMA a cor do próprio chapéu, quem vai ser a primeira pessoa a descobrir a cor do próprio chapéu? Tente resolver por conta própria antes de ler a resposta que está no final do texto.
A ideia é simples, quem descobre a cor do seu chapéu usa o fato de saber que os outros não sabem para conseguir deduzir a cor. No caso, foi dado um Conhecimento Comum (2) de que há um chapéu vermelho e as pessoas usam o fato das pessoas saberem isso para inferirem novas informações. Mas se para esse pequeno problema lógico dos Chapéus Vermelhos a resposta já pode ser confusa… imagina quando as situações se tornam mais complexas! Esse pequeno exemplo foi só para ilustrar um dos jogos mais interessantes estudados pela Economia Comportamental, o Concurso de Beleza! Também conhecido como Acerte a Média!

Figura 2: Conhecimento Comum também tem piada e eu sei que você não achou graça.
3 Acerte a Média
Pense na seguinte situação. Um grupo de pessoas está jogando um jogo que tem a seguinte regra. Todos podem falar um número de 0 a 100. Ganham prêmios aquelas pessoas que falarem o número mais próximo de 2/3 da média de todos os números que fazem parte do jogo, i.e. todos os números que essas pessoas do grupo falaram. O premio é 1000 reais dividido por todos aqueles que acertaram o número. Qual número você falaria?
Conhecimento Comum se torna uma coisa complexa e fundamental nesse jogo.
Vamos supor que normalmente, as pessoas consideram que a média de números aleatórios entre 0 e 100 seja 50. (Vamos começar com 50, mas poderíamos começar com qualquer número. Num grupo de N pessoas, se todos falarem 50, todos ganhariam 1000 reais dividido por N e ficariam todos felizes. Mas a gente pode tentar arrumar um jeitinho de ganhar os 1000 tentando jogar um número menor que os dos adversários. Você sabe que normalmente a média seria 50, então seria melhor jogar algo próximo de 2/3 de 50, algo como 33…
Mas, já que temos Conhecimento Comum, a gente sabe que as pessoas sabem que você sabe, que você pensaria em jogar 33… então seria melhor jogar 2/3 de 33. 22 talvez? Mas Conhecimento Comum vai além, todo mundo sabe que todo mundo sabe ad infinitum. De 22, iriamos para 14, de 14 para 9, de 9 para 6…e assim chegaríamos em todo mundo jogando 0 3.
Essa é a única resposta por Conhecimento Comum e infelizmente não conseguimos dar um jeito de ganhar os 1000 reais. Este jogo ilustra uma diferença fundamental entre a racionalidade perfeita de um agente e o Conhecimento Comum sobre a racionalidade entre os agentes. Mesmo que os jogadores sejam perfeitamente racionais nesse jogo, se deveria chutar 0. Isso só acontece caso eles saibam que os outros jogadores também são racionais e que a racionalidade de todos os jogadores é de conhecimento comum.
Mas será que as pessoas realmente fazem isso?
4 Cognição de Level K
Tente sua sorte numa simulação online:
E ai, você acertou? Se você leu o texto após a sua tentativa já tem uma boa ideia do que é Cognição de Level K. Preste muita atenção no gráfico abaixo (4):
Tem muita gente doida no mundo. Tem alguns malucos que chutam 100 (espero que não tenha sido você)… vai entender o que se passa na cabeça dessa (sua) pessoa. Contudo, perceba que mesmo no meio dessa loucura, existem pelo menos 4 grandes grupos (5) de pessoas. O primeiro grupo que está chutando números perto de 50, o segundo grupo que está chutando números perto de 33, o terceiro grupo chutando número perto de 22 e o quarto perto de 0. Esse tipo de agrupamento é o que Cognição de level k discute.
Cognição de Level K descreve quantos passos nós damos dentro dessas interações infinitas do Conhecimento Comum. O primeiro grupo de pessoas que chuta em torno de 50 não dá nenhum passo. Esse caso é chamado de Cognição de level 0. Essas pessoas não percebem que se alguém chutar um número abaixo delas, eles perdem o jogo.
O segundo grupo dá um passo, sabem que as pessoas sabem. Isso significa que elas acreditam que as pessoas entenderam o jogo, mas não que as pessoas sabem que sabem. Assim, elas imaginam que as pessoas chutariam algo em torno de 50 e por isso chutam 33. Denominado assim Cognição de level 1.
O terceiro grupo, de cognição level 2, é o mais predominante, elas sabem que as pessoas sabem que as pessoas sabem, chutando assim 22.
O grupo perto zero é provavelmente formado por aqueles que estudaram Teoria dos Jogos e tentaram ser espertos mas perderam porque não perceberam que as pessoas não estudaram Teoria dos Jogos. Triste.
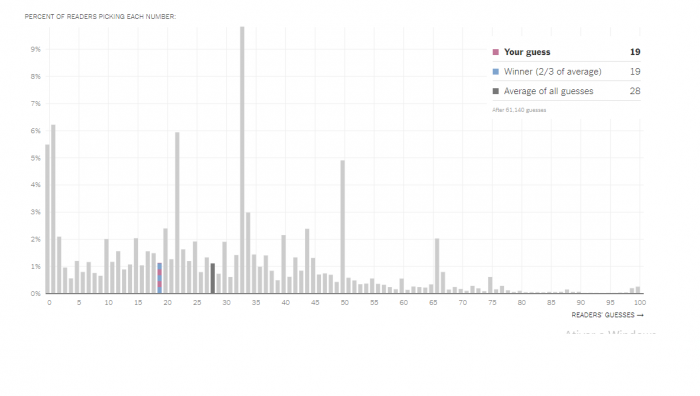
Figura 3: Tentativa das pessoas no site do nytimes
Perceba que a interação entre esses grupos criam soluções que muito provavelmente ficam entre os grupos e diferentes distribuições de pessoas podem levar a diferentes respostas. Não há assim uma resposta certa de cara e o meu 19 foi sorte mesmo. Por exemplo: em um mundo em que todos fazem cognição de level 0, todos empatariam. Mas se tiver uma pessoa que faz mais interações, ela ganharia sozinha. Ao mesmo tempo, se quase todos estão no level 0 (num grupo de 8 ou mais) e existem duas pessoas, uma de level 1 e outra de level 2, a level 1 seria aquela que ganharia. (6)
Outra interessante observação é que se as pessoas continuarem a jogar esse jogo repetidamente, eventualmente todos aprendem a jogar zero. Há um aprendizado e eventualmente todo mundo fica craque em Teoria dos Jogos.
5 Conclusão
Entre Jogos e Comportamentos existe um mundo cheio de interessantes observações que nos ajudam a entender como o mundo funciona. Lógica nos dá ferramentas interessantes para descobrimos as melhores escolhas. Mas quando a lógica se torna demandante demais, como em alguns casos do Conhecimento Comum, o que fazemos é procurar soluções de meio termo (heurísticas) para conseguir tomar alguma decisão e assim há comportamentos como a cognição de level k. É sempre bom notar que no mundo real o que parece ser irracional é muitas vezes o mais racional.
Solução:
A resposta: A terceira pessoa será a primeira e a única pessoa a identificar a cor do próprio chapéu!
Vamos tentar dar a resposta completa analisando mais casos; primeiramente analisaremos a situação que encontramos com 3 chapéus vermelhos, depois falaremos do caso completo. O número representa a pessoa (1, 2 ou 3), B branco e V vermelho:
• Ao ver dois vermelhos, 1 não sabe se está de branco ou vermelho.
– 1 saberia a cor do próprio chapéu se visse dois brancos (2B-3B).
Nesse caso, todo mundo saberia diretamente quem tem cada chapéu de cada cor (1V-2B-3B) pois é a única maneira do branco descobrir e os outros agentes sabem disso por Conhecimento Comum. Como 1 não sabe, não pode ter visto dois brancos e estamos em uma dessas situações (2B-3V; 2V-3V; 2V-3B).
• 2 sabe que 1 não sabe a cor dos próprio chapéu então estamos entre as opções (2B-3V; 2V-3V; 2V-3B). Aos ver dois vermelhos (1V-3V), não sabe em qual situação 1 estava (2V-3V; 2B-3V), não dando para saber qual é a cor do próprio chapéu.
– Se 2 visse 1B-3V, novamente não daria para saber em qual situação estamos e podemos ter (2V-3V; 2B-3V). Restariam duas situações. Se 2 viesse 1B-3B, ela automaticamente saberia que é a única pessoa de chapéu vermelho. Se 2 visse 1V-3B e sabendo que 1 não viu 2B (pois se não 1 saberia a cor do próprio chapéu) ela deduziria que ela está de vermelho. Isso significa que dado que 1 não sabe e supondo 3 estivesse de branco, 2 teria certeza da cor do seu chapéu vermelho. Mais do que isso, 3 sabendo que 2 sabe, também saberia que seu
chapéu é branco.
• Ao ver 1V-2V e sabendo que nenhum dos outros dois sabem que a cor do próprio chapéu a única possibilidade é todos de chapéu vermelho.
– 1V-2B-3B foi excluído porque 1 não sabe. 1V-2V-3B e 1B-2V-3B são excluídos porque 2 não sabe a cor do próprio chapéu. Temos as opções 1B-2B-2V, 1B-2V-3V, 1V-2B-3V e 1V-2V-3V. Como 3 vê 1V-2V, ela sabe que está nessa última opção (1V-2V-3V.)
Algo interessante de se constatar é que mesmo que 3 saiba perfeitamente em qual situação está, a informação de que 3 sabe qual é a cor do próprio chapéu não ajuda 1 ou 2 excluir novas possibilidades.
A citação lá do início é do criador da Teoria dos Jogos. Ele está correto?
Citações:
Artigos e livros:
Aumann, Robert J. (1976). Agreeing to Disagree (PDF). The Annals of Statistics. 4 (6): 1236–1239.
Newman, P. (1992). Common Knowledge and the Game of Red Hats. Indian Economic Review, 27, 451-457.
Camerer, C. F., Ho, T. H., & Chong, J. K. (2004). A cognitive hierarchy model of games. The Quarterly Journal of Economics, 119(3), 861-898.
Nagel, R. (1995). Unraveling in guessing games: An experimental study. The American Economic Review, 85(5), 1313-1326.
Moulin, Herve (1986). Game Theory for the Social Sciences (2nd ed.). New York: NYU Press.
Dixit, A. K., Nalebuff, B. (2008). The art of strategy: a game theorist’s guide to success in business life. WW Norton Company.
Nash, John (1951) Non-Cooperative Games The Annals of Mathematics 54(2):286-295.
Websites:
https://www.nytimes.com/interactive/2015/08/13/upshot/are-you-smarterthan-other-new-york-times-readers.html
https://pt.wikipedia.org/wiki/Teoria_dos_jogos
Notas
1. Se não conhece, fica aqui a sugestão de um livro que ilustra a área: The art of Strategy do Avinash K. Dixit.
2 Fica aqui a de título de ilustração que esse fato em si pode ser considerado um Conhecimento Mútuo que é uma forma mais franca de Conhecimento Comum, mas para se chegar à resposta é necessária a interação entre esse conhecimento das pessoas(i.e. conhecimento comum).
3 Que, por sinal, é o único Equilíbrio de Nash desse jogo.
4 Note que como eu sou um bom economista comportamental eu acertei o meu chute. Ou sou sortudo…
5 Existem outros grupos menores, mas vamos usar esses 4.
6 Momento Jogos Evolucionários: Não é o mais inteligente que ganha, é o mais adaptado ao ambiente.

